Domain Adaption for 3D Point Cloud Segmentation using Active Learning Strategies

Duration of the Thesis: 6 months
Completition: September 2020
Supervisor: M.Sc. Michael Kölle, Dr.-Ing. Volker Walter
Examiner: Prof. Dr.-Ing. Uwe Sörgel

It is universally acknowledged that we are living in a time of information exploration. Every day mass data is generated and needed to be processed. However, the more common situation is that we can easily acquire a mass of data while do not have enough corresponding labelled samples. Considering this, a possible solution would be active learning (AL). It is designed to label as fewer samples as possible but to reach as higher accuracy as possible. Furthermore, even though different task usually has different datasets, they could be related or similar in a way. Aimed at saving time and energy, domain adaption (DA) is used between two datasets in this situation. It transfers knowledge which can be useful both in the source domain and the target domain. With this adaption, we have a chance to take advantage of what we already have instead of just discarding old work each time.

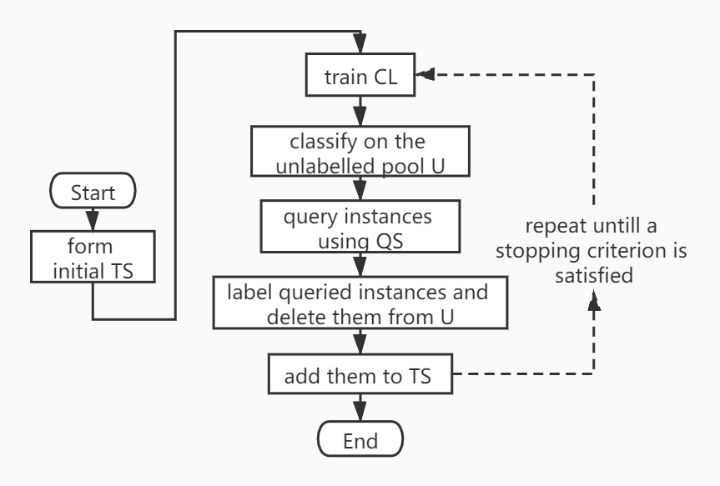
To test the merit of active learning and domain adaption, we apply these two methods with two 3D points clouds datasets acquired in Vaihingen and Hessigheim. We firstly do active learning in Vaihingen which is our source domain. The workflow is shown in Figure 1. In the beginning, there is assumed no labelled sample. The initial training set is formed by picking 10 points per class randomly and assigning labels to them. Then a random forest classifier is trained to give predictions for the rest samples.

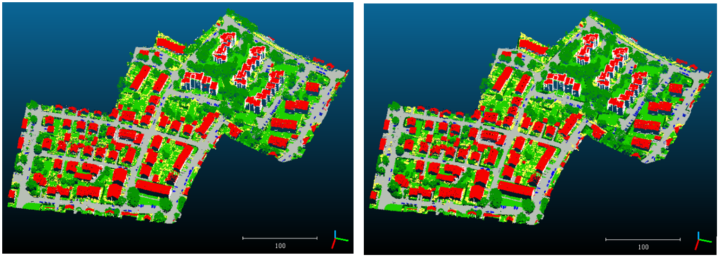
We use pool-based AL and the individual query strategy is random sampling, entropy-based sampling and breaking tie sampling. Each time we query and label 300 instances and add them to the training set. After 30 iterations, breaking tie sampling has the best performance. The prediction result is shown in Figure 2. Compared to the true data, there is no much deviation.

In domain adaption, SVM is adopted to detect the most certain classified source samples, then we use the optimal transfer (OT) to minimize the global cost from the source to the target domain. Firstly, we calculate l-2 norm between each pair of instances from the source and target domain respectively to get the cost matrix C. Then a sparse matrix 𝛾 is generated with the same size of C. Nonzero values between 0 and 1 are assigned to positions where we have matches. Thirdly, each source sample has a distance to its hyperplane in SVM. The certainty of a target sample is the sum of the distances from the source samples it matched normalized by the number of source samples it matched. The best-matched target samples are to be added to the training set for active learning in the target domain.

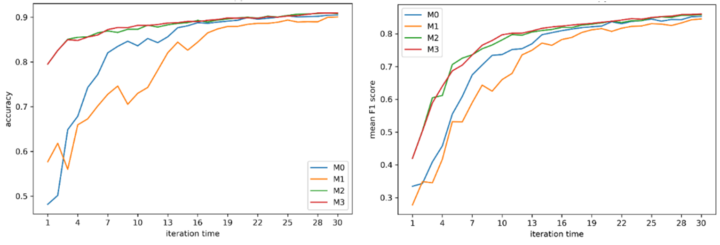
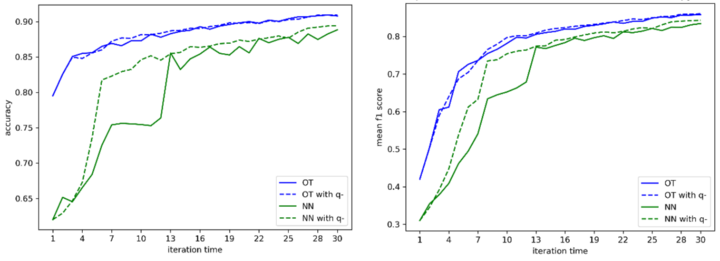
In the target domain, we have four methods. Hyperparameters are the same as these insource domain. M0 is exactly what we have done in the target domain just switching from source to target dataset. M1 changes the initial training set from 10 points per class to the final TS in the source domain. M2 is added with the OT results compared to M1. M3 is added with a query function q- to remove the non-representative source samples. The nearest neighbour (NN) transfer is also adopted to prove the advantage of OT. The results show that optimal transfer can dramatically increase the prediction accuracy compared with other methods. For example, the results of entropy-based sampling are shown in Figure 3 and Figure 4.

In the end, we switch the role of source and target domain and do the whole process again to test the validity of OT. The results are in the same pattern as before indicating OT is a universal method.

Angluin D. Query and concept learning [J]. Machine learning, 1988, 2(4): 319-342.

Cohn, L. Atlas, and R. Ladner. Improving generalization with active learning. Machine Learning, 15(2):201–221, 1994.